蚌埠网站制作公司费用电子报刊的传播媒体是什么

Hello！大家好，我是@学霸小羊，今天先来讲讲约瑟夫问题的背景。

在古罗马时期，犹太历史学家约瑟夫斯领导犹太人反对罗马帝国的统治，并与罗马军队进行激烈的战斗。然而，在罗马军队的围困下，约瑟夫与其士兵被困在一个山洞里，总共有41人。约瑟夫希望向罗马军队投降，但他的士兵却视死如归，拒绝投降。约瑟夫陷入了困境，因为如果他表达投降的意愿，士兵们很可能会杀掉他。面对这种局面，约瑟夫需寻找一种能够确保自己安全的解决办法。

约瑟夫找到了士兵们都能接受的解决方案：让大家围成一个圈，按照顺时针的顺序杀掉旁边的人，一轮一轮地进行，直到最后只剩下一个人。通过这种方法，约瑟夫能够实现投降的目的，同时也能保证自己的安全。士兵们都认为这个办法可行，并按照约瑟夫的要求行动起来。

约瑟夫问题的解决过程：

1、初始情况

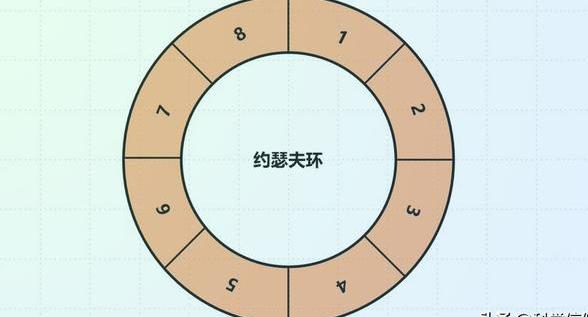
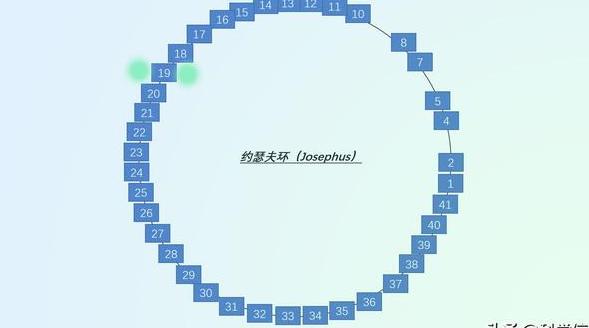
在山洞中，约瑟夫站在第19号位置上，而其他40名士兵围成一个圈。按照约瑟夫的要求，每人依次杀掉旁边的人，直到只剩下约瑟夫和另外一名士兵。

2、第一轮

第一轮开始，1号士兵杀掉了2号士兵，然后3号士兵杀掉了4号士兵，以此类推。经过这一轮，20名士兵被杀死，还剩下21人。

3、第二轮

第二轮开始，1号士兵杀掉了3号士兵，然后5号士兵杀掉了7号士兵，以此类推。经过这一轮，10名士兵被杀死，还剩下11人。

4、第三轮

第三轮开始，1号士兵杀掉了5号士兵，然后9号士兵杀掉了11号士兵，以此类推。经过这一轮，5名士兵被杀死，还剩下6人。

5、第四轮

第四轮开始，1号士兵杀掉了9号士兵，然后17号士兵杀掉了19号士兵，以此类推。经过这一轮，2名士兵被杀死，还剩下3人。

6、最后一轮

到了最后一轮，1号士兵杀掉了17号士兵，留下了约瑟夫和最后一名士兵。而约瑟夫选择不杀掉最后一名士兵，而是劝说他一同投降。

7、成功的解决办法

通过这种数学方法，约瑟夫成功地解决了困境，实现了投降的目的。最后的幸存者序号就是约瑟夫的当前位置，他通过精确计算，站在第19号位置上，并顺利地获救了。

约瑟夫问题的规律

经过对约瑟夫问题的思考和探索，约瑟夫总结出了一条规律：在参与游戏的总人数为2的n次幂时，最后的幸存者一定是1号；而当总人数不满足2的n次幂时，最后的幸存者序号为2a1，其中a是大于参与人数的最大2的n次幂。

这个规律其实也可以通过归纳法进行证明。假设参与人数为2的n次幂a时，最后的幸存者是1号，现在有2的n次幂a1个人参与，那么可以将其拆分为两部分：一部分为2的n次幂a的人数，另一部分为剩下的那个人。而根据上述规律，2的n次幂a这部分人最后的幸存者一定是1号。然后再将这两部分合并在一起，那么最后的幸存者序号就变成了合并后剩下这个人的序号，即2a1。

总结

约瑟夫问题给我们展示了数学在现实生活中的应用之一。通过利用数学方法解决困境，约瑟夫成功地实现了自己的目标。这个问题不仅考验了数学思维能力，还需要有创新和决策的能力。约瑟夫通过巧妙地控制整个游戏的进行，最终使自己获得了胜利。

而对我个人来说，约瑟夫问题也给我带来了一些思考。人类的生活中经常会遇到各种难题和困境，解决这些问题需要我们灵活运用知识和技能，找到最适合的方法和策略。而数学，作为一门综合性学科，提供了丰富的思维模式和解决思路，可以帮助我们更好地理解和应对困境。

以约瑟夫为例，他通过对问题的深入思考和分析，发现了其中的规律，并应用数学原理解决了困境。这给我们提供了一个启示，即在面对问题时，我们可以尝试从不同的角度和思维方式出发，寻找到更加创新和有效的解决办法。

而总体来说，约瑟夫问题不仅考察了数学的应用能力，还锻炼了我们的逻辑思维、分析问题和决策能力。通过学习和思考这个问题，我们不仅可以提升自己的数学素养，还能培养出更加全面的综合能力，为未来的学习和工作打下坚实的基础。所以，要善于运用数学思维解决问题，探索出更多的可能性，为自己的成长和发展创造更广阔的空间。

好啦，今天就先讲到这，拜拜！