当前位置： 首页 > news >正文

本地的镇江网站建设chrome浏览器下载安卓手机

news 2025/7/1 8:47:04
本地的镇江网站建设,chrome浏览器下载安卓手机,无锡定制网站,域名停靠黄金网页推广方案什么是树 一种分层数据的抽象模型。前端工作中常见的树包括：DOM树，级联选择，树形控件JS中没有树，可以用Object和Array构建树树的常用操作：深度/广度优先遍历，先中后序遍历 深度优先遍历 访问根节点对根节…

什么是树

  • 一种分层数据的抽象模型。
  • 前端工作中常见的树包括：DOM树，级联选择，树形控件
  • JS中没有树，可以用Object和Array构建树
  • 树的常用操作：深度/广度优先遍历，先中后序遍历

深度优先遍历

  • 访问根节点
  • 对根节点的children挨个进行深度优先遍历

代码展示：

const tree = {val: 'a',children: [{val: 'b',children: [{val: 'd',children: []},{val: 'e',children: []}]},{val: 'c',children: [{val: 'f',children: []},{val: 'g',children: []}]}],
};const dfs = (root) => {console.log(root.val);root.children.forEach(dfs);
}dfs(tree);

输出顺序：a -> b -> d -> e -> c -> f -> g

广度优先遍历

  • 新建一个队列，把根节点入队
  • 把队头出队并访问
  • 把队头的children分别入队
  • 重复二，三步，直到队列为空

代码展示：

const bfs = (root) => {const q = [root];while (q.length) {const n = q.shift();console.log(n.val);n.children.forEach((child) => {q.push(child);})}
}bfs(tree);

输出顺序：a -> b -> c -> d -> e -> f -> g

先序遍历

  • 访问根节点
  • 对根节点的左子树进行先序遍历
  • 对根节点的右子树进行先序遍历

代码展示：

const bt = {val: 1,left: {val: 2,left: {val: 4,left: null,right: null},right: {val: 5,left: null,right: null}},right: {val: 3,left: {val: 6,left: null,right: null},right: {val: 7,left: null,right: null}}
};
// 递归
const preorder = (root) => {if (!root) return;console.log(root.val);preorder(root.left);preorder(root.right);
}preorder(tree);// 迭代
const preorder = (root) => {if (root) return;const stack = [root];while (stack.length) {const n = stack.pop();console.log(top.val);if (n.right) stack.push(n.right);if (n.left) stack.push(n.left);}}
}preorder(tree);

参考视频：传送门

输出顺序：1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7

中序遍历

  • 对根节点的左子树进行中序遍历
  • 访问根节点
  • 对根节点的右子树进行中序遍历

代码展示：

// 递归
const inorder = (root) => {if (!root) return;preorder(root.left);console.log(root.val);preorder(root.right);
}inorder(tree);// 迭代
const inorder = (root) => {if (!root) return;const stack = [];let p = root;while (stack.length || p) {while (p) {stack.push(p);p = p.left;}const n = stack.pop();console.log(n.val);p = n.right;}
}inorder(tree);

输出顺序：4 -> 2 -> 5 -> 1 -> 6 -> 3 -> 7

后序遍历

  • 对根节点的左子树进行后序遍历
  • 对根节点的右子树进行后序遍历
  • 访问根节点

代码展示：

// 递归
const postorder = (root) => {if (!root) return;preorder(root.left);preorder(root.right);console.log(root.val);
}postorder(tree);// 迭代
const postorder = (root) => {if (!root) return;const stack = [root];const outputStack = [];while (stack.length) {const n = stack.pop();outputStack.push(n);if (n.left) stack.push(n.left);if (n.right) stack.push(n.right);}while (outputStack) {const n = outputStack.pop();console.log(n.val);}
}postorder(tree);

输出顺序：4 -> 5 -> 2 -> 6 -> 7 -> 3 -> 1

leetcode题目

难度：简单

  1. 二叉树的最大深度

思路：

  • 求最大深度，优先考虑深度优先遍历
  • 在深度优先遍历过程中，记录每个节点所在的层级，找到最大的层级即可

代码展示：

/*** @param {TreeNode} root* @return {number}*/
var maxDepth = function(root) {let maxDepth = 0;const dfs = (n, l) => {if (!n) return;dfs(n.left, l + 1);dfs(n.right, l + 1);if (!n.left && !n.right) maxDepth = Math.max(maxDepth, l);}dfs(root, 1);return maxDepth;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点个数。

  • 空间复杂度：O(height)：height为二叉树的最大深度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(logN)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

  1. 翻转二叉树

思路：

  • 方法一使用广度优先遍历，在遍历树的过程中，交换当前层级下的左右子树
  • 方法二使用递归解决，递归最重要的是定义子问题。

代码展示：

方法一：广度优先遍历

/*** @param {TreeNode} root* @return {TreeNode}*/
var invertTree = function(root) {if (!root) root;const bfs = (root) => {const q  = [root];while (q.length) {const n = q.shift();const temp = n.right;n.right = n.left;n.left = temp;if (n.left) q.push(n.left);if (n.right) q.push(n.right);}}bfs(root);return root;
}

方法二：递归

/*** @param {TreeNode} root* @return {TreeNode}*/
var invertTree = function(root) {if (!root) return null;let newTree = new TreeNode(root.val);newTree.left = invertTree(root.right);newTree.right = invertTree(root.left);return newTree;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点个数。

  • 空间复杂度：O(height)：height为二叉树的最大深度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(logN)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

  1. 对称二叉树

思路：

  • 通过遍历比较两个相同根节点的左子树和右子树的值是否相等
  • 如果每次都相等，直到两个节点都不存在，说明是对称的
  • 如果两个节点不相等，则说明不对称

代码展示：

/** * @param {TreeNode} root * @return {boolean} */
var isSymmetric = function(root) {if (!root) return false;const checkSym = (p, q) => {if (!p && !q) return true;if (!p || !q) return false;return p.val === q.val && checkSym(p.left, q.right) && checkSym(q.left, p.right);}return checkSym(root, root);
}

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)：n为二叉树节点数，最差情况为O(n)。

  1. 二叉树的直径

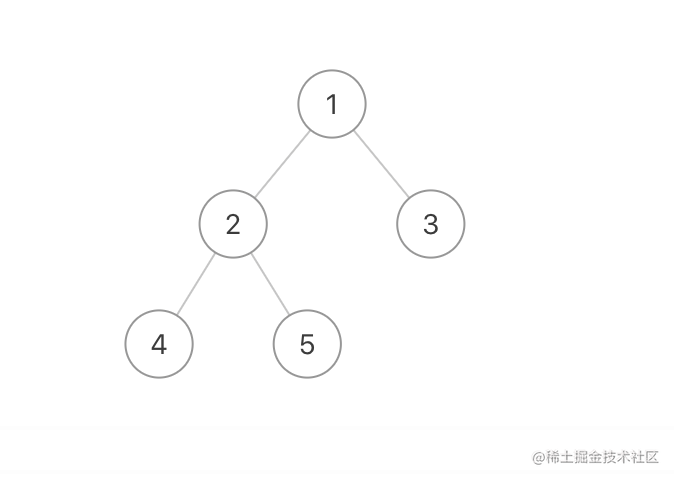
在这里插入图片描述

思路：

  • 考虑深度优先遍历
  • 寻找两个最深的节点距离之和

代码展示：

/*** @param {TreeNode} root* @return {number}*/
var diameterOfBinaryTree = function(root) {if (!root) return 0;let res = 1; // 默认为根节点的路径长度const dfs = (root) => {if (!root) return 0;let L = dfs(root.left);  // 左子树深度，上图为例，最长L为2let R = dfs(root.right);  // 右子树深度，上图为例，最长R为1res = Math.max(res, L + R + 1); // 最大L+R+1，+1为根节点，总共深度为4，即节点树为4return Math.max(L, R) + 1;  // 包含根节点的深度，上图为例，最长L为2，最长R为1}dfs(root);return res - 1; // 最终结果要得到直径为3
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(height)：height为二叉树的最大深度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(logN)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

剑指 Offer 27. 二叉树的镜像

思路：

  • 逐层递归互换左右子树节点的位置

代码展示：

/*** @param {TreeNode} root* @return {TreeNode}*/
var mirrorTree = function(root) {if (!root) return root;const temp = root.left;root.left = root.right;root.right = temp;mirrorTree(root.left);mirrorTree(root.right);return root;
}

优化后：

/** * @param {TreeNode} root * @return {TreeNode} */
var mirrorTree = function(root) {if (!root) return root;[root.left, root.right] = [mirrorTree(root.right), mirrorTree(root.left)];return root;
}

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)：n为二叉树节点树。

  1. 二叉树的最近公共祖先

剑指 Offer 68 - II. 二叉树的最近公共祖先

思路：

  • 递归

代码展示：

/** * @param {TreeNode} root * @param {TreeNode} p * @param {TreeNode} q * @return {TreeNode} */
var lowestCommonAncestor = function(root, p, q) {// 当传入递归的树等于 p 或者等于 q，说明找到了 p 或者 q，返回给递归调用的 l 或 rif (!root || p === root || q === root) return root;let l = lowestCommonAncestor(root.left, p, q); // 递归调用，寻找 p 和 qlet r = lowestCommonAncestor(root.right, p, q); // 递归调用，寻找 p 和 qreturn l && r ? root : l || r; // 如果 p 和 q 分别在 root.left 和 root.right 中找到，则根节点 root 成为最近的公共祖先返回。// 假如 p 和 q 在 root.left 中找到，递归会把 p 和 q 的公共祖先返回给 l。// 假如，p 和 q 在 root.right 中找到，递归会把 p 和 q 的公共祖先返回给 r。// 根节点root，l 或 r 最终成为当前函数的返回值。
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(n)：n为二叉树节点数。递归调用的栈深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为 N，因此空间复杂度为 O(N)。

剑指 Offer 55 - I. 二叉树的深度

思路：

  • 考虑深度优先遍历

代码展示：

var maxDepth = function (root) {if (!root) return 0;let max = 0;const dfs = (root, l) => {if (root.left) dfs(root.left, l + 1);if (root.right) dfs(root.right, l + 1);if (!root.left && !root.right) max = Math.max(max, l);}dfs(root, 1);return max;
}

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数，计算树的深度需要遍历所有节点。

  • 空间复杂度：O(n)：最差情况下，空间复杂度为O(n)。

  1. 二叉树的所有路径

思路：

  • 本题考虑使用深度优先遍历。
  • 如果当前节点有左子树或右子树，就递归调用函数，直到左右子树都不存在，此时就是我们要找的的路径。

代码展示：

/*** @param {TreeNode} root* @return {string[]}*/
var binaryTreePaths = function(root) {if (!root) return [];const res = [];const dfs = (root, path) => {if (root) {path += root.val;if (!root.left && !root.right) {res.push(path);} else {path += '->';dfs(root.left, path);dfs(root.right, path);}}}dfs(root, "");return res;
};

复杂度分析：

  • 时间复杂度：O(n^2)：n为二叉树节点数。在深度优先搜索中每个节点会被访问一次且只会被访问一次，每一次会对 path 变量进行拷贝构造，时间代价为 O(N)，故时间复杂度为 O(N^2)。
  • 空间复杂度：O(n^2)：n为二叉树节点数。

剑指 Offer 32 - I. 从上到下打印二叉树

剑指 Offer 32 - II. 从上到下打印二叉树 II

  • 解题方法同二叉树的层序遍历
  1. 平衡二叉树

思路：

  • 考虑深度优先遍历

  • 算出最大深度和最小深度的差值，即可判断是否为平衡二叉树 (本题和求二叉树直径做法类似)

代码展示：

/*** @param {TreeNode} root* @return {boolean}*/
var isBalanced = function(root) {if (!root) return true;let diff = 0;const dfs = (root) => {if (!root) return 0;let L = dfs(root.left);let R = dfs(root.right);diff = Math.max(diff, Math.abs(R - L));return Math.max(L, R) + 1;}dfs(root);return diff - 1 <= 0;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)：n为二叉树节点数，最差情况为O(n)。

  1. 合并二叉树

思路：

  • 递归对两个相同位置的节点相加

代码展示：

/*** @param {TreeNode} root1* @param {TreeNode} root2* @return {TreeNode}*/
var mergeTrees = function(root1, root2) {if (!root1 || !root2) return root1 || root2;let newRoot = new TreeNode(root1.val + root2.val);newRoot.left = mergeTrees(root1.left, root2.left);newRoot.right = mergeTrees(root1.right, root2.right);return newRoot;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)：n为二叉树节点数。

  1. 路径总和

思路：

  • 考虑深度优先遍历
  • 记录从根节点到当前节点的和，与target比较。

代码展示：

/** * @param {TreeNode} root * @param {number} targetSum * @return {boolean} */
var hasPathSum = function(root, targetSum) {if (!root) return false;let res = false;const dfs = (root, val) => {if (root.left) dfs(root.left, val + root.left.val);if (root.right) dfs(root.right, val + root.right.val);if (!root.left && !root.right && val === targetSum) res = true;}dfs(root, root.val);return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)：n为二叉树节点数。

  1. 二叉树的最小深度

思路：

  • 方法一考虑使用广度优先遍历

  • 方法二考虑使用深度优先遍历

代码展示：

方法一：

/*** @param {TreeNode} root* @return {number}*/
var minDepth = function(root) {if (!root) return 0;let minDep = Infinity;const bfs = (root, l) => {const q = [[root, l]];while (q.length) {const [n, l] = q.shift();if (n.left) q.push([n.left, l + 1]);if (n.right) q.push([n.right, l + 1]);if (!n.left && !n.right) minDep = Math.min(minDep, l);}}bfs(root, 1);return minDep;
};

方法二：

/** * @param {TreeNode} root * @return {number} */
var minDepth = function(root) {if (!root) return 0;if (root.left && root.right) {return 1 + Math.min(minDepth(root.left), minDepth(root.right));} else if (root.left) {return 1 + minDepth(root.left);} else if (root.right) {return 1 + minDepth(root.right);} else {return 1;}
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)：n为二叉树节点数。

  1. N 叉树的前序遍历

思路：

  • 类似于二叉树的前序遍历

代码展示：

// 递归
var preorder = function(root) {if (!root) return [];const res = [];const preord = (n) => {if (n) res.push(n.val);n.children.forEach(preord);}preord(root);return res;
};// 迭代
var preorder = function(root) {if (!root) return [];const stack = [root];const res = [];while (stack.length) {const n = stack.pop();res.push(n.val);n.children.reverse().forEach(child => {stack.push(child);});}return res;
}

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(height)：height为二叉树最大深度。

剑指 Offer 54. 二叉搜索树的第k大节点

思路：

  • 根据树的特点，采用中序遍历，按右子树 - 根节点 - 左子树的顺序遍历，就可以由大到小找到第k大节点

代码展示：

/*** @param {TreeNode} root* @param {number} k* @return {number}*/
var kthLargest = function(root, k) {if (!root || k <= 0) return null;const stack = [];const res = null;let p = root;while (stack.length || p) {while (p) {stack.push(p);p = p.right;}const top = stack.pop();if (--k === 0) return top.val;p = top.left;}return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(n)：n为二叉树节点数。

难度：中等

  1. 二叉树的前序遍历

代码展示：

/*** @param {TreeNode} root* @return {number[]}*/
var preorderTraversal = function(root) {if (!root) return [];const stack = [root];const res = [];while (stack.length) {const n = stack.pop();res.push(n.val);if (n.right) stack.push(n.right);if (n.left) stack.push(n.left);}return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)

  1. 二叉树的中序遍历

代码展示：

/*** @param {TreeNode} root* @return {number[]}*/
var inorderTraversal = function(root) {if (!root) return [];const stack = [];const res = [];let p = root;while (stack.length || p) {while (p) {stack.push(p);p = p.left;}const n = stack.pop();res.push(n.val);p = n.right;}return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)

  1. 二叉树的后序遍历

代码展示：

/*** @param {TreeNode} root* @return {number[]}*/
var postorderTraversal = function(root) {if (!root) return [];const stack = [root];const outputStack = [];const res = [];while (stack.length) {const n = stack.pop();outputStack.push(n);if (n.left) stack.push(n.left);if (n.right) stack.push(n.right);}while (outputStack.length) {const n = outputStack.pop();res.push(n.val);}return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)

  1. 二叉树的层序遍历

代码展示：

方法一：深度优先遍历

/*** @param {TreeNode} root* @return {number[][]}*/
var levelOrder = function(root) {if (!root) return [];const res = [];const dfs = ([root, l]) => {if (!res[l]) {res[l] = [root.val];} else {res[l].push(root.val)}if (root.left) dfs([root.left, l + 1]);if (root.right) dfs([root.right, l + 1]);}dfs([root, 0]);return res;
};

方法二：广度优先遍历

/*** @param {TreeNode} root* @return {number[][]}*/
var levelOrder = function(root) {if (!root) return [];let res = [];const bfs = (root, l) => {const q = [[root, l]];while (q.length) {const [n, l] = q.shift();if (!res[l]) res[l] = [];res[l].push(n.val);if (n.left) q.push([n.left, l + 1]);if (n.right) q.push([n.right, l + 1]);}};bfs(root, 0);return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)

  1. 从前序与中序遍历序列构造二叉树

  2. 从中序与后序遍历序列构造二叉树

剑指 Offer 07. 重建二叉树

思路：

  • 递归

代码展示：

参考：多种解法，逐渐优化

/*** @param {number[]} preorder* @param {number[]} inorder* @return {TreeNode}*/
var buildTree = function(preorder, inorder) {if (!preorder.length || !inorder.length) return null;const map = new Map();for (let i = 0; i < inorder.length; i++) {map.set(inorder[i], i);}const builder = (p_start, p_end, i_start, i_end) => {if (p_start > p_end) return null;let rootVal = preorder[p_start]; // 找到根节点let root = new TreeNode(rootVal); // 设置二叉树的根节点let mid = map.get(rootVal);  // 找到根节点在inorder中的位置let leftNum = mid - i_start; // 左子树的个数root.left = builder(p_start + 1, p_start + leftNum, i_start, mid - 1);root.right = builder(p_start + leftNum + 1, p_end, mid + 1, i_end);return root;}return builder(0, preorder.length - 1, 0, inorder.length - 1);
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)

  1. 二叉树的锯齿形层序遍历

思路：

  • 同二叉树层序遍历

代码展示：

/*** @param {TreeNode} root* @return {number[][]}*/
var zigzagLevelOrder = function(root) {if (!root) return [];const res = [];const bfs = ([root, index]) => {if (!root) return;if (!res[index]) {res[index] = [root.val];} else {index % 2 === 0 ? res[index].push(root.val) : res[index].unshift(root.val);}if (root.left) bfs([root.left, index + 1]);if (root.right) bfs([root.right, index + 1]);}bfs([root, 0]);return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)

  1. 二叉树的右视图

思路：

  • 方法一考虑广度优先遍历，每层保留最后一个元素

  • 方法二考虑使用类似先序遍历，根 - 右 - 左的方式遍历，每层第一个出现的元素保留下来即可

代码展示：

方法一：广度优先遍历

/*** @param {TreeNode} root* @return {number[]}*/
var rightSideView = function(root) {if (!root) return [];const res = [];const bfs = (root, l) => {const q = [[root, l]]while (q.length) {const [n, l] = q.shift();res[l] = n.val;if (n.left) q.push([n.left, l + 1]);if (n.right) q.push([n.right, l + 1]);}}bfs(root, 0);return res;
};

方法二：

/*** @param {TreeNode} root* @return {number[]}*/
var rightSideView = function(root) {if (!root) return [];const res = [];const stack = [[root, 0]];while (stack.length) {const [n, l] = stack.pop();if (res[l] == undefined) res.push(n.val);if (n.left) stack.push([n.left, l + 1]);if (n.right) stack.push([n.right, l + 1]);}return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(n)

剑指 Offer 26. 树的子结构

思路：

  • 递归比较

代码展示：

/** * @param {TreeNode} A * @param {TreeNode} B * @return {boolean} */
var isSubStructure = function(A, B) {if (!A || !B) return false;const isSameSub = (p, q) => {if (!q) return true;if (!p) return false;if (p.val !== q.val) return false;return isSameSub(p.left, q.left) && isSameSub(p.right, q.right);}return isSameSub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
};

复杂度分析：

  • 时间复杂度：O(mn)：m，n分别为A和B的节点数。

  • 空间复杂度：O(m)

  1. 验证二叉搜索树

代码展示：

/** * @param {TreeNode} root * @return {boolean} */
var isValidBST = function(root) {const helper = (root, lower, upper) => {if (root === null) {return true;}if (root.val <= lower || root.val >= upper) {return false;}return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);}return helper(root, -Infinity, Infinity);
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(n)

  1. 不同的二叉搜索树

思路：

  • 卡塔兰数公式

代码展示：

var numTrees = function(n) {let C = 1;for (let i = 0; i < n; ++i) {C = C * 2 * (2 * i + 1) / (i + 2);}return C;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。

  • 空间复杂度：O(1)

  1. 完全二叉树的节点个数

代码展示：

/** * @param {TreeNode} root * @return {number} */
var countNodes = function(root) {return root ? countNodes(root.left) + countNodes(root.right) + 1 : 0;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(1)

剑指 Offer 34. 二叉树中和为某一值的路径

代码展示：

/*** @param {TreeNode} root* @param {number} target* @return {number[][]}*/
var pathSum = function(root, target) {if (!root) return [];const res = [];let temp = [];const dfs = (root, v) => {if (!root) return null;temp.push(root.val);if (root.left) dfs(root.left, root.left.val + v);if (root.right) dfs(root.right, root.right.val + v);if (!root.left && !root.right && v === target) {res.push([...temp]);}temp.pop();}dfs(root, root.val);return res;
};

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(n)

难度：困难

  1. 二叉树中的最大路径和

代码展示：

参考解法

/*** @param {TreeNode} root* @return {number}*/
var maxPathSum = function(root) {let maxNum = Number.MIN_SAFE_INTEGER;const dfs = (root) => {if (!root) return 0;const left = dfs(root.left);const right = dfs(root.right);const curMaxSum = left + root.val + right; // 当前子树内部最大路径和maxNum = Math.max(maxNum, curMaxSum);const outputMaxSum = root.val + Math.max(left, right); // 当前子树对上一层输出的最大路径和return outputMaxSum > 0 ? outputMaxSum : 0; // 大于0有输出的必要，小于0就返回0};dfs(root);return maxNum;
}

复杂度分析：

  • 时间复杂度：O(n)：n为二叉树节点数。
  • 空间复杂度：O(n)

剑指 Offer 37. 序列化二叉树

总结

继续对树的深度/广度优先遍历，先中后序遍历，层序遍历等遍历和递归的方法，有更深入的理解和学习。

http://www.wooajung.com/news/28566.html

相关文章：

  • 仓库出入库管理系统东莞百度seo排名
  • 网站推广公司百度首页排名优化价格
  • 做物流行业网站的开发公司谈谈你对网络营销的看法
  • 中国顶级网站建设seo点击工具
  • 网站敏感词汇seo顾问合同
  • 学校做的网站外面访问不了怎么找拉新推广平台
  • 怎么做游戏网站的宣传图片seo教学视频教程
  • 草桥做网站公司seo公司厦门
  • 开源手机网站建站系统站长之家素材网
  • 分析旅游网站的功能河源市企业网站seo价格
  • 张家口网站网站建设网络营销学什么内容
  • 广州网站建设报价seo技术培训学校
  • 做网站的参考文献有哪些b2b外链
  • 怎么用织梦做本地网站百度怎么推广自己的网站
  • 网站建设合同书范本简单的网页设计作品
  • 湖北省级建设主管部门网站外贸seo站
  • 免费加盟一件代发货源网站百度163黄页关键词挖掘
  • 网站建设方案怎么做seo搜索优化
  • 怎样开发网站建设seo是什么职位的简称
  • 能看人与动物做的网站手机怎么建网站
  • 纺织服装板块上市公司网站建设外包公司到底值不值得去
  • 婴儿网站建设住栏目seo优化包括
  • 灰色网站网站的推广优化
  • 广州做网站的企业网络培训心得
  • 快速网站推广公司seo技术外包公司
  • 网站建设广州天河区优化师是一份怎样的工作
  • 网站制作怎么做图标厦门关键词优化报价
  • 用python做的电商网站网站开发软件
  • 重庆网站建设外包公司哪家好百度助手免费下载
  • 电子商务网站主要面向百度如何优化排名靠前