1. 堆栈基础知识

1.1 堆栈简介

1. 定义
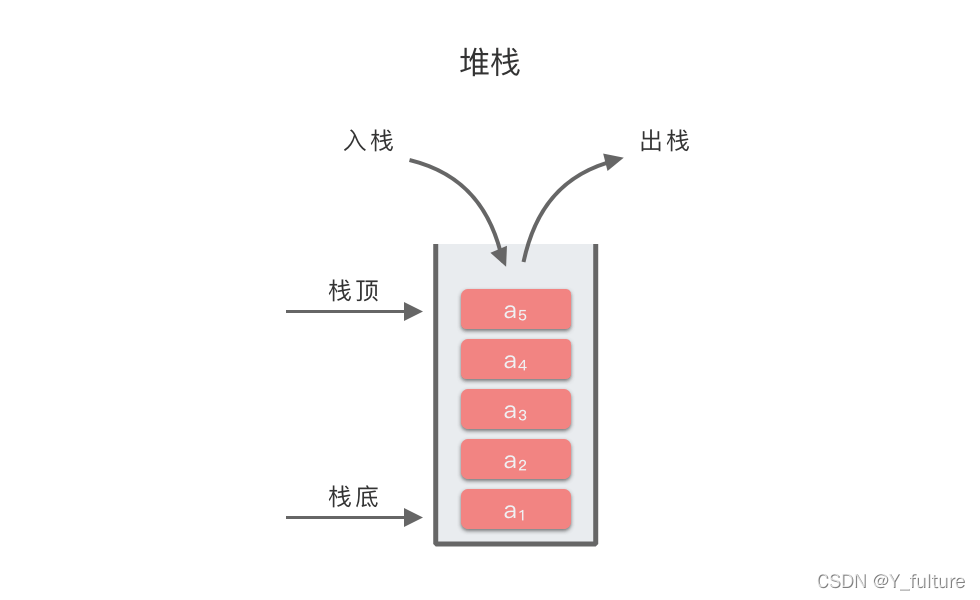
   堆栈（Stack）：简称为栈。一种线性表数据结构，是一种只允许在表的一端执行插入和删除操作的线性表。
   栈顶（Top）：栈中允许插入和删除的一端
   栈底（Bottom）：不是栈顶的另一端
   空栈：没有任何元素的栈
2. 特点：后进先出（Last In First Out），即LIFO结构
3. 相关解释
   1. 线性表：栈首先是一个线性表，栈中元素具有前驱后继的线性关系。栈中元素按照次序依次进栈
   2. 根据堆栈的定义，每次删除的总是堆栈中当前的栈顶元素，即最后进入堆栈的元素。而在进栈时，最先进入堆栈的元素一定在栈底，最后进入堆栈的元素一定在栈顶
      

1.2 堆栈的顺序存储与链式存储

与线性表的顺序存储和链式存储相似，栈也有两种存储方法：顺序栈和链式栈

1. 顺序栈：即堆栈的顺序存储结构。利用一组地址连续的存储单元依次存放自栈底到栈顶的元素，同时使用指针 top 指示栈顶元素在顺序栈中的位置。
2. 链式栈：即堆栈的链式存储结构。利用单链表的方式来实现堆栈。栈中元素按照插入顺序依次插入到链表的第一个节点之前，并使用栈顶指针 top 指示栈顶元素，top 永远指向链表的头节点位置

1.2.1 堆栈的基本操作

1. 初始化空栈：创建一个空栈，定义栈的大小 size，以及栈顶元素指针 top
2. 判断栈是否为空：当堆栈为空时，返回 True。当堆栈不为空时，返回 False。
   一般只用于栈中删除操作和获取当前栈顶元素操作中
3. 判断栈是否已满：当堆栈已满时，返回 True，当堆栈未满时，返回 False。
   一般只用于顺序栈中插入元素和获取当前栈顶元素操作中
4. 插入元素（进栈、入栈）：相当于在线性表最后元素后面插入一个新的数据元素，并改变栈顶指针 top 的指向位置
5. 删除元素（出栈、退栈）：相当于在线性表最后元素后面删除最后一个数据元素，并改变栈顶指针 top 的指向位置
6. 获取栈顶元素：相当于获取线性表中最后一个数据元素。与插入元素、删除元素不同的是，该操作并不改变栈顶指针 top 的指向位置

1.2.2 堆栈的顺序实现（利用List）

1. 基本描述
   
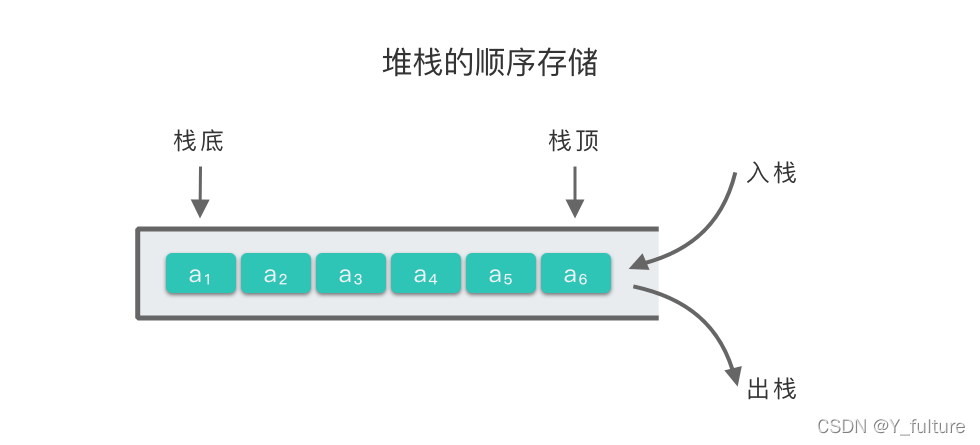
   1. 初始化空栈：创建一个空的列表，并定义栈的大小self.size，并令栈顶元素指针self.top指向-1，即self.top = -1
   2. 判断栈是否为空：当 self.top == -1 时，说明堆栈为空，返回 True，否则返回 False
   3. 判断栈是否已满：当 self.top == self.size - 1，说明堆栈已满，返回 True，否则返回返回 False
   4. 获取栈顶元素：先判断队列是否为空，为空直接抛出异常。不为空则返回 self.top 指向的栈顶元素，即 self.stack[self.top]
   5. 入栈:先判断队列是否已满，已满直接抛出异常。如果队列未满，则在 self.stack 末尾插入新的数据元素，并令 self.top 向右移动 1 位
   6. 出栈:先判断队列是否为空，为空直接抛出异常。如果队列不为空，则令 self.top 向左移动 1 位，并返回 self.stack[self.top]
2. 代码实现：

   class Stack:# 初始化空栈def __init__(self, size = 100):self.stack = []self.size = sizeself.top = -1# 判断栈是否为空def is_empty(self):return self.top == -1# 判断栈是否已满def is_full(self):return self.top + 1 == self.size# 入栈def push(self, val):if self.is_full():raise Exception('Stack is full')else:self.stack.append(val)self.top += 1# 出栈操作def pop(self):if self.is_empty():raise Exception("Stack is empty")else:self.stack.pop()self.top -= 1# 获取栈顶元素def peek(self):if self.is_empty():raise Exception("Stack is empty")else:return self.stack[self.top]		
   

1.2.3 堆栈的链式实现

1. 基本描述：

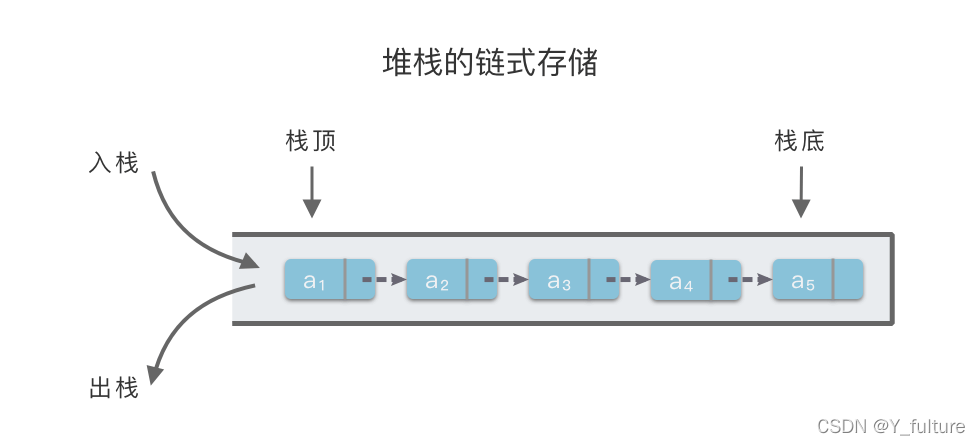
   1. 初始化空栈：使用列表创建一个空栈，并令栈顶元素指针 self.top 指向 None，即 self.top = None
   2. 判断栈是否为空：当 self.top == None 时，说明堆栈为空，返回 True，否则返回 False
   3. 获取栈顶元素：先判断队列是否为空，为空直接抛出异常。不为空则返回 self.top 指向的栈顶节点，即 self.top.value。
   4. 入栈:创建值为 value 的链表节点，插入到链表头节点之前，并令栈顶指针 self.top 指向新的头节点。
   5. 出栈:先判断队列是否为空，为空直接抛出异常。如果队列不为空，则令 self.top 链表移动 1 位，并返回 self.top.value]

2. 代码实现：

   # 先定义链节点
   class Node:def __init__(self, val):self.val = valself.next = None
   # 定义栈
   class Stack:# 初始化空栈def __init__(self):self.top = None# 判断栈是否为空def is_empty(self):return self.top == None# 查看栈顶元素def peek(self):if self.is_empty():raise Exception("Stack is empty")else:self.top.val# 入栈def push(self, val):cur = Node(val)cur.next = self.topself.top = cur# 出栈def pop(self):if self.is_empty():raise Exception('Stack is empty')else:cur = self.topself.top = self.top.nextdel cur
   

1.3 堆栈的常见应用

1. 使用堆栈可以很方便的保存和取用信息，因此长被用作算法和程序中的辅助存储结构，临时保存信息，供后面操作中使用
2. 堆栈的后进先出规则，可以保证特定的存取顺序

2. 堆栈与深度优先搜索

2.1 深度优先算法简介

1. 深度优先搜索算法（Depth First Search）：英文缩写为 DFS。是一种用于遍历或搜索树或图的算法。该算法沿着树的深度遍历树的节点，会尽可能深的搜索树的分支。当节点 v 的所在边都己被探寻过，搜索将回溯到发现节点 v 的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

   深度优先搜索使用的是回溯思想，这种思想很适合使用「递归」来实现。而递归对问题的处理顺序，遵循了「后进先出」的规律。所以递归问题的处理，需要借助「堆栈」来实现

   在深度优先遍历的过程中，我们需要将当前遍历节点 v 的相邻节点暂时存储起来，以便于在回退的时候可以继续访问它们。遍历到的节点顺序符合「后进先出」的特点，所以深度优先搜索可以通过「递归」或者「堆栈」来实现

2.2 基于递归实现深度优先搜索

1. 步骤:
   1. graph 为存储无向图的字典变量，visited 为标记访问节点的 set 集合变量。start 为当前遍历边的开始节点。def dfs_recursive(graph, start, visited): 为递归实现的深度优先搜索方法
   2. 将 start 标记为已访问，即将 start 节点放入 visited 中（visited.add(start)）
   3. 访问节点 start，并对节点进行相关操作（看具体题目要求）
   4. 访问节点 start，并对节点进行相关操作（看具体题目要求）
      如果 end 没有被访问过，则从 end 节点调用递归实现的深度优先搜索方法，即 dfs_recursive(graph, end, visited)
2. 代码实现:

def dfs_recursive(graph, start, visited):# 标记节点visited.add(start)# 访问节点print(start)for end in graph[start]:if end not in visited:dfs_recursive(graph, start, visited)

2.3 基于堆栈实现深度优先搜索

1. 步骤:
   1. start 为开始节点。定义 visited 为标记访问节点的 set 集合变量。定义 stack 用于存放临时节点的栈结构
   2. 首先访问起始节点，并对节点进行相关操作（看具体题目要求）
   3. 然后将起始节点放入栈中，并标记访问。即 visited = set(start)，stack = [start]
   4. 如果栈不为空，取 stack 栈顶元素 node_u
   5. 遍历与节点 node_u 相连并构成边的节点 node_v
      • 如果 node_v 没有被访问过，则：
        1. 访问节点 node_v，并对节点进行相关操作（看具体题目要求）
        2. 将 node_v 节点放入栈中，并标记访问，即 stack.append(node_v)，visited.add(node_v)
        3. 跳出遍历 node_v 的循环
      • 继续遍历 node_v
   6. 如果 node_u 相邻的节点都访问结束了，从栈顶弹出 node_u，即 stack.pop()
   7. 重复步骤 4 ~ 6，直到 stack 为空
2. 代码实现:

def dfs_stack(graph, start):print(start)                        # 访问节点 startvisited = set(start)                # 使用 visited 标记访问过的节点，先标记 startstack = [start]                     # 创建一个栈，并将 start 加入栈中while stack:node_u = stack[-1]              # 取栈顶元素i = 0while i < len(graph[node_u]):   # 遍历栈顶元素，遇到未访问节点，访问节点并跳出。node_v = graph[node_u][i]if node_v not in visited:   # node_v 未访问过print(node_v)           # 访问节点 node_vstack.append(node_v)    # 将 node_v 加入栈中visited.add(node_v)     # 标记为访问过 node_vbreaki += 1if i == len(graph[node_u]):    # node_u 相邻的节点都访问结束了，弹出 node_ustack.pop()

3. 相关题目

3.1 堆栈相关题目

150.逆波兰表达式求值

class Solution:def evalRPN(self, tokens: List[str]) -> int:def evalute(nums1, nums2, token):if token == '+':return nums1 + nums2elif token == '-':return nums2 - nums1elif token == '*':return nums1 * nums2elif token == '/':return int(nums2 / nums1)stack = []for token in tokens:try:stack.append(int(token))except:nums1 = stack.pop()nums2 = stack.pop()stack.append(evalute(nums1, nums2, token))return stack[0]

394.字符串解码

946.验证栈序列

3.2 深度优先搜索相关题目

200.岛屿数量

class Solution:def numIslands(self, grid: List[List[str]]) -> int:def dfs(grid, r, c):visited.add((r,c))nr, nc = len(grid), len(grid[0])for x, y in [(r - 1, c), (r + 1, c), (r, c + 1), (r, c - 1)]:if 0 <= x < nr and 0 <= y < nc and grid[x][y] == '1' and (x, y) not in visited:dfs(grid, x, y)nr = len(grid)if nr == 0:return 0nc = len(grid[0])num_island = 0visited = set()for r in range(nr):for c in range(nc):if grid[r][c] == '1' and (r, c) not in visited:num_island += 1dfs(grid, r, c)return num_island