---

1. 左式堆概述

为了有效支持合并操作，即以 $o(N)$ 时间进行 Merge ，我们需要使用动态的链接结构或者静态链表。如果只使用数组形式的堆结构，在进行合并时光拷贝一个数组到另一个数组中，就将花费 $\Theta (N)$ 的时间。

左式堆 (leftist tree, leftist heap ），或者说左偏堆、左偏树，是一种优先队列实现方式，属于可并堆(除了左式堆外，还有如斜堆、二项堆、配对堆、斐波那契堆等)。在统计问题、最值问题、模拟问题和贪心问题等等类型的题目中，都有着广泛的应用。

左式堆和二叉堆一样具有结构性质和堆序性质，它具有和其他堆一样的堆序性质，同时也是一棵二叉树。和二叉堆唯一的区别在于：左式堆是很不平衡的。

2. 左式堆性质

为了完全了解左式堆的性质，我们需要以下定义：

• 外结点：只有一个儿子或没有儿子的节点，即左右儿子至少有一个为空节点的节点。
• 距离/零路径长 null path length ：npl(X) 定义为 X 结点到它的后代中离它最近的外结点的最短路径长度，即两结点之间路径的权值和。特别的，外结点的距离为 0 ，空结点的距离为 npl(NULL) = -1 。
• 左偏树/左式堆：一种满足左偏性质的堆有序的二叉树，其左偏性质体现在左儿子的距离大于等于右儿子的距离。
• 左偏树/左式堆的距离：我们将一棵左偏树根结点的距离作为该树的距离。

左式堆的基本性质如下：

• 满足堆的基本性质，如小根堆中，结点的键值小于等于其左右儿子结点的键值
• 对于任意结点，左儿子的距离大于等于右儿子的距离
• 对于任意结点，其距离等于它右儿子的距离加一
• 一个距离为 $d$ 的左式堆，其结点数必然不小于 $2^{d+1}-1$ 个结点
• 对于一个有 $n$ 个结点的左式堆，其根结点的距离不超过 $\log n$

下图中，距离或者说 null path length 标记在结点内部。很明显，只有左边的树是左式的，因为它之中任何结点左儿子的距离都大于等于右儿子的距离：

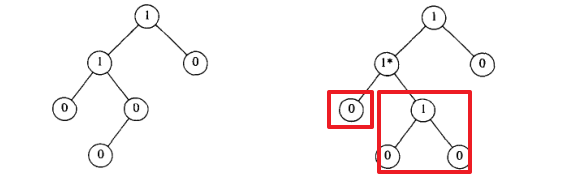
左式堆性质：对于堆中的任意结点 X ，其左儿子的距离至少与右儿子的距离一样长。任一结点的距离，都比它的诸儿子结点的距离的最小值(就是右儿子的距离)多 1 。

上述性质不仅确保了树平衡的要求，而且偏重于使树向左增加深度，甚至很可能存在由左结点形成的长路径构成的树，在实际上更有利于合并操作——因此，得名左式堆 leftist heap 。

由于左式堆倾向于增长左路径，所以右路径应该短。甚至，沿着左式堆右侧的右路径是该堆中最短的路径。不然，就存在一条路径通过某个结点 X 向左儿子深入，X 就破坏了左式堆的左偏性质。

定理：在右路径上有 $r$ 个结点的左式堆必然至少存在 $2^r-1$ 个结点。或者说，一个距离为 $d$ 的左式堆，其结点数必然不小于 $2^{d+1}-1$ 个结点。

证明：数学归纳法证明。

• 如果 $r=1$ ，则必然至少存在一个树结点。
• 设定理对 $1,2,\dots ,r$ 个结点成立。考虑在右路径上有 $r+1$ 个结点的左式树。此时，根具有在右路径上含有 $r$ 个结点的右子树，以及在右路径上至少含有 $r$ 个结点的左子树（否则就不是左式堆）。对这两个子树应用归纳假设，可知每棵子树上最少有 $2^r-1$ 个结点，加上根结点，于是该树上最少有 $2^{r+1}-1$ 个结点。
  
  

从这个定理可知，对于一个有 $n$ 个结点的左式堆，其根结点的距离，即右路径最多含有 $\lfloor \log (n+1)\rfloor$ 个结点。

---

3. 左式堆操作和代码实现

对左式堆操作的一般思路是：将所有的工作放到右路径进行，从而保证树的深度更短。不过，对于右路径的 insert, merge 可能破坏左式堆性质。尽管恢复起来也很容易。

左式堆可能有的基本结点信息，具体实现时可以酌情添加和修改：

• $val$ ：键值
• $left$ ：左儿子
• $right$ ：右儿子
• $dist$ ：距离
• $father$ ：父亲

左式堆的C++结构：

#include <bits/stdc++.h>
using namespace std;template <typename Comparable>
class LeftistHeap {
private:struct LeftistNode {Comparable element;  //数据值 LeftistNode *left;   //左儿子 LeftistNode *right;  //右儿子 int dist;			 //距离 LeftistNode(const Comparable &theElement, LeftistNode *lt = nullptr, LeftistNode *rt = nullptr, int d = 0): element(theElement), left(lt), right(rt), dist(d) { }};LeftistNode *root;LeftistNode *merge(LeftistNode *h1, LeftistNode *h2);  	//私有的合并方法 LeftistNode *merge1(LeftistNode *h1, LeftistNode *h2);  //实际执行的merge方法 void swapChildren(LeftistNode *t);						//交换左右子树	//void reclaimMemory(LeftistNode *t);						//LeftistNode *clone(LeftistNode *t) const;
public:LeftistHeap();							//建立空堆 LeftistHeap(const LeftistHeap &rhs);	//复制rhs建堆 ~LeftistHeap();							//析构函数 bool empty() const;				   		//判断是否为空 const Comparable &findMin() const; 		//找到最小值 void insert(const Comparable &x);  		//插入:合并单结点和堆即可 void deleteMin();				   		//删除最小值 void deleteMin(Comparable &minItem); 	//删除并返回最小值 void makeEmpty();				   		//清空左式堆 void merge(LeftistHeap &rhs);	   		//公共的合并方法 const LeftistHeap& operator=(const LeftistHeap &rhs); //赋值运算符函数 
};

(1) 合并操作

左式堆最基本也最重要的操作是合并，毕竟是可并堆。下面介绍一个简单的递归算法，输入是两个左式堆 $H_1,H_2$ ，如下图，这两个堆都是左式堆，而且是小根堆：

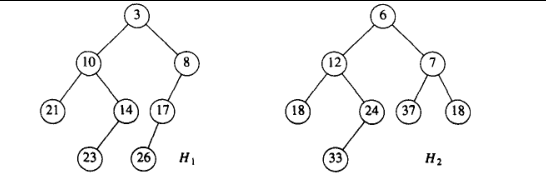
如果两个堆中有一个堆为空，就直接返回另一个堆。否则为了合并两个堆，需要比较它们的根。首先，递归将根值较大的堆和根值较小的堆的右子堆合并。这里递归地将 $H_2$ 与 $H_1$ 中根值为 $8$ 的右子堆合并，得到下图的堆：

这棵树是递归形成的，虽然现在不知道是如何得到的，不过处理基准情形后，我们假设递归步骤能够成立，合并可以完成。接着要让这个新的堆成为 $H_1$ 的根的右儿子：

这时的堆满足堆序性质，但不满足左偏性质，不是左式堆。可以看出其根结点的左子树的距离为 $1$ ，而根的右子树的距离为 $2$ 。左式堆的性质在根处被破坏。

但是树的其余部分必然是左式的，由于递归步骤，根的右子树是左式的，左子树没有变化还是左式的。所以，只要对根进行调整就好了。为了让整个树都是左式的，交换树根的左儿子和右儿子，并更新根结点的距离，新的距离是新的右儿子的距离加一，这样就完成了 merge 。

可以手动模拟这个过程，就能够知道这个递归算法如何运行了。步骤总结如下：(函数 merge(x, y) 表示合并 x, y ，返回值是合并后的根结点)

• 如果有一个根结点是空，则返回另一个根结点；
• 设 x 是 x, y 中权值较小的那个，即 $va{l}_x\le va{l}_y$ 。若 x 的权值大于 y，交换 x, y 进行合并即可；
• 为了维护小根性质，合并好的堆的堆顶一定还是 x ，所以递归向下合并 x 的子树（左右都行，一般用右子树）和 y ；
• 递归结束后，y 和 x 的右子树形成一个新的左式堆，其结果成为 x 的新的右子树；
• 合并后可能破坏 x 的左偏性质，所以需要检查 x 此时左右子树的距离，如果左子树的距离小于右子树，就交换左右子树，更新 x 的距离为新的右子树的距离加一。

代码如下：

//公有的merge方法将rhs合并到已有的优先队列(左式堆),rhs成为空堆 
void LeftistHeap::merge(LeftistHeap &rhs) {//rhs必须和this不同if (this == &rhs) return; //不接受h.merge(h) root = merge(root, rhs.root); //调用私有的merge方法merge(h1, h2); rhs.root = nullptr;           //rhs的root指向空 
}
//内部方法合并两个根,消除一些特殊情形,保证H1有较小根; 
//作为驱动程序调用merge1进行实际的合并 
LeftistNode *merge(LeftistNode *h1, LeftistNode *h2) {if (h1 == nullptr) return h2;if (h2 == nullptr) return h1; if (h1->element < h2->element) //保证h1是较小的根 return merge1(h1, h2); else return merge1(h2, h1);
}
//merge1进行实际的合并和距离的调整 
LeftistNode *merge1(LeftistNode *h1, LeftistNode *h2) {if (h1->left == nullptr) //单结点h1->left = h2; 	     //h1的其他部分已经准确了else {h1->right = merge(h1->right, h2);if (h1->left->dist < h1->right->dist) swapChildren(h1);h1->dist = h1->right->dist + 1;}return h1;
}

执行合并的时间与右路径的长的和成正比。因此，合并两个左式堆的时间为 $\text{O(logN)}$ 。

(2) 插入操作

插入只是合并的特殊情况，可以看成是单结点堆和更大的堆的 merge。

void insert(const Comparable &x) { //push,新建一个新结点和堆合并即可root = merge(new LeftistNode(x), root);
}

(3) 删除最小值操作

由于是小根堆，可以除掉根从而得到两个堆，接着将两个堆进行合并即可。执行一次 deleteMin 操作的时间是 $\text{O(logN)}$ 。

void deleteMin() {if (empty()) throw underflow_error("LeftistHeap Empty");LeftistNode *oldRoot = root;root = merge(root->left, root->right);delete oldRoot;
}void deleteMin(Comparable &minItem) {minItem = findMin();deleteMin();
}