当前位置：首页 > news >正文

浅析 manacher（马拉车）算法

news 2025/7/27 13:36:41

哈喽大家好，我是 doooge，今天给大家带来的是浅析 manacher（马拉车）算法

\[\Huge \sf 浅析~manacher（马拉车）算法 \]

1. manacher 算法是什么

先给一道例题（P3805）：

给定一个字符串 \(S\)，求 \(S\) 中最长的回文串的长度。
\(|S|\le 1.1\times 10^7\)。

容易想到的写法是暴力枚举 \(S\) 的每一个字串，再判断子串是否是回文串，复杂度 \(O(n^3)\)，明显达不到要求。

我们试着优化这个暴力算法：

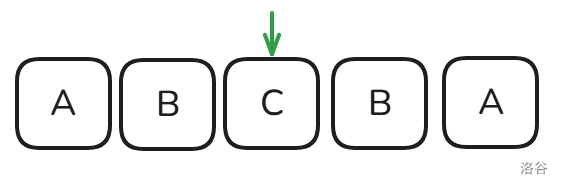
我们知道，一个字符串要是长度为奇数的一个回文串，必须要有一个中心的字符，并且使中心左右两侧的字符对称：

那要是有字符串的长度是偶数的呢？我们可以试着用 | 把字符串隔开：

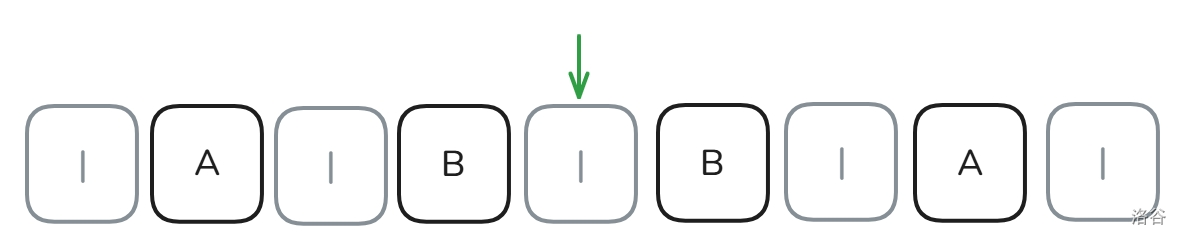
这样就能让长度强制为奇数了。

我们是不是能枚举每个字符作为一个回文串的中心，再暴力向两边拓展，这样的事件复杂度就是 \(O(n^2)\) 的了，但是还是达不到标准。

于是，我们的 manacher 算法就派上用场了！

2. 正文：manacher 算法匹配过程

声明：\(S_{l,r}\) 表示 \(S\) 从 \(l\) 到 \(r\) 的子串

首先我们先定义 \(p_i\) 表示以 \(i\) 作为中心最长的对称的回文串的半径，就像这样：

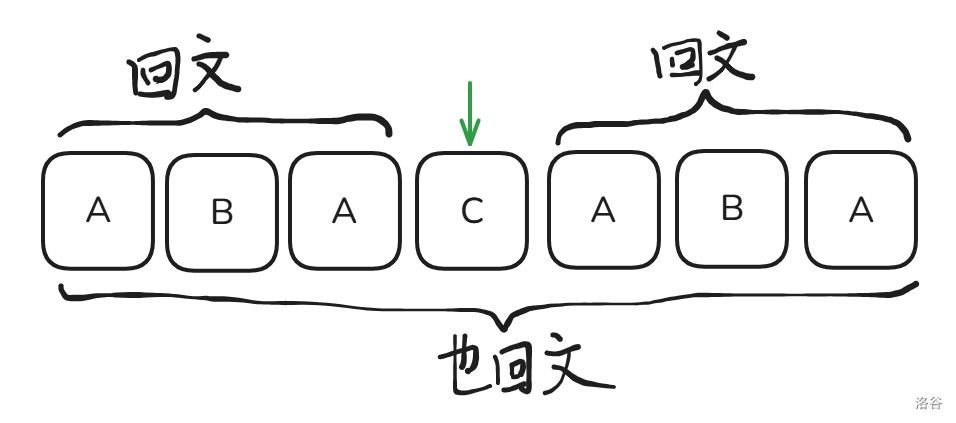
（\(mid\) 为箭头指的那个，也就是整个串的中心）

不难发现 \(S_{mid-p_{mid},mid+p_{mid}}\) 回文，且 \(S_{mid-p_{mid},mid}=S_{mid,mid+p_{mid}}\)，而且，我们设 \(S_{mid-p_{mid},mid}\) 这个子串的中心为 \(i\)，\(S_{mid,mid+p_{mid}}\) 的中心为 \(j\)，那么就有 \(S_{i-p_i}=S_{j,j+p_j}\)，这就是 manacher 的核心思想

在匹配过程中，我们定义 \(R\) 为扫到的最右边的位置，\(mid\) 为包括 \(r\) 的最右边的中心，例如：

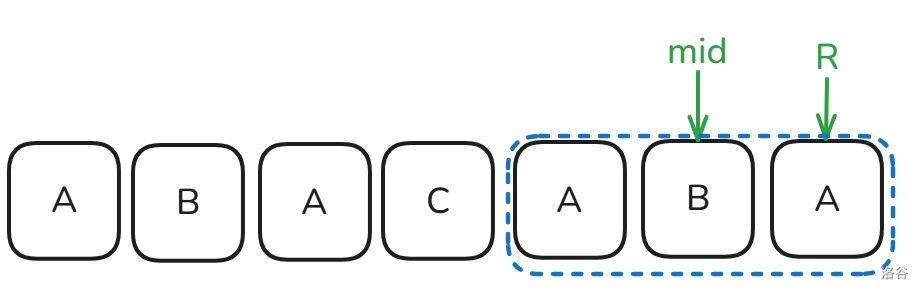
我们发现，当我们求 \(p_i\) 的时候，有两种情况：

\(i\) 在 \(mid\) 到 \(R\) 区间内：我们不难发现，因为中间这个串是回文的，所以对于 \(S_{mid,i}\)，我们可以找出一个对称点 \(j\)，满足 \(S_{i-p_i,i+p_i}\) 和 \(S_{j-p_j,j+p_j}\) 对称，所以可以这样转移：

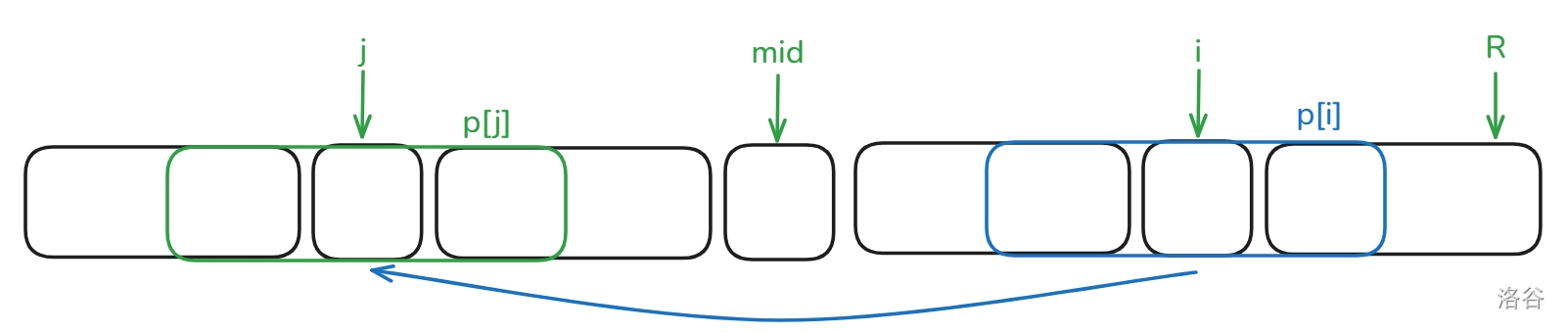
注意从 \(S_{j-p_j,j+p_j}\) 转移过来有可能越界，所以我们要在这里多加判断

\(i>R\)，这时暴力拓展即可

答案就是 \(\max p_i-1\) 了。

每次拓展完毕时我们更新 \(R\) 和 \(mid\)，由于 \(R\) 指针只能向后移，所以时间复杂度是 \(O(n)\) 的。

注意：为了防止越界，应该在 \(S\) 的前面和后面分别加一个特殊字符 ~ 和 #

3. manacher 的代码

#include<bits/stdc++.h>
using namespace std;
int p[22000010];
char s[22000010];
int main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);int cnt=0,mid=0,R=0,ans=0;char c=' ';s[++cnt]=c,s[++cnt]='|';//防止越界 while(cin>>c){//读入 s[++cnt]=c,s[++cnt]='|';}s[++cnt]='#';//同样防止越界 for(int i=2;i<=cnt-1;i++){//注意i从2开始到cnt-1 if(i<=R){//i不可能<=mid，这个请自行体会 p[i]=min(p[(mid<<1)-i],R-i+1);//mid*2-i就是i的对称点 }else{p[i]=1;}while(s[i-p[i]]==s[i+p[i]]){//暴力拓展 p[i]++;}if(i+p[i]>R){//更新R和mid R=i+p[i]-1,mid=i;}ans=max(ans,p[i]-1);}cout<<ans<<endl;return 0;
}